结构体对齐详解

发布时间：2014-1-16 17:28
分类名称：C++


From: http://www.cnblogs.com/motadou/archive/2009/01/17/1558438.html

注释：本文通过仔细阅读，还是发现一些问题。在此，我总结出更加精炼的法则：

1. 对齐数据成员，对齐模数为：#pragma pack指定的数值以及该数据成员自身长度中数值较小者。对齐成员有两种，一种是普通数据类型，一种的结构体类型。结构体的长度计算为：结构体内部最大的基本数据类型成员长度。所以即便是结构体类型，对齐模数也同样适用。如果觉得复杂，可以先将所有的结构体平铺展开，再计算。

2. 所有的数据成员对齐后，再对齐最外层的结构体，如何对齐？还是参加第一条。再一次声明：结构体的长度计算为：结构体内部最大的基本数据类型成员长度。取该长度和#pragma pack指定的数值中数值较小者。

还要记住一文章中的那张表：

  

  

char

short

int

long

double

long

double

Windows

长

度

1

2

4

4

8

8

模

数

1

2

4

4

8

8

Linux

长

度

1

2

4

4

8

12

模数

1

2

4

4

4

4

就OK了。

 

以下是原文：

1 -- 结构体数据成员对齐的意义
许多实际的计算机系统对基本类型数据在内存中存放的位置有限制，它们会要求这些数据的起始地址的值是某个数k的倍数，这就是所谓的内存对齐，而这个k则被称为该数据类型的对齐模数(alignment modulus)。这种强制的要求一来简化了处理器与内存之间传输系统的设计，二来可以提升读取数据的速度。比如这么一种处理器，它每次读写内存的时候都从某个8倍数的地址开始，一次读出或写入8个字节的数据，假如软件能保证double类型的数据都从8倍数地址开始，那么读或写一个double类型数据就只需要一次内存操作。否则，我们就可能需要两次内存操作才能完成这个动作，因为数据或许恰好横跨在两个符合对齐要求的8字节内存块上。
2 -- 结构体对齐包括两个方面的含义
1)结构体总长度
2)结构体内各数据成员的内存对齐，即该数据成员相对结构体的起始位置
3 -- 结构体大小的计算方法和步骤
1)将结构体内所有数据成员的长度值相加，记为sum_a；
2)将各数据成员为了内存对齐，按各自对齐模数而填充的字节数累加到和sum_a上，记为sum_b。对齐模数是#pragma pack指定的数值以及该数据成员自身长度中数值较小者。该数据相对起始位置应该是对齐模式的整数倍;
3)将和sum_b向结构体模数对齐，该模数是#pragma pac指定的数值和结构体内部最大的基本数据类型成员长度中数值较小者。结构体的长度应该是该模数的整数倍。
4 -- 结构体大小计算举例
在计算之前，我们首先需要明确的是各个数据成员的对齐模数，对齐模数和数据成员本身的长度以及pragma pack编译参数有关，其值是二者中最小数。如果程序没有明确指出，就需要知道编译器默认的对齐模数值。下表是Windows XP/DEV-C++和Linux/GCC中基本数据类型的长度和默认对齐模数。
 

  

  

char

short

int

long

double

long double

Windows

长度

1

2

4

4

8

8

模数

1

2

4

4

8

8

Linux

长度

1

2

4

4

8

12

模数

1

2

4

4

4

4

 
例子1：
struct my_struct
{
char a;
long double b;
};
此例子Windows和Linux计算方法有些许不一致。

在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B = 9B --> sum_a = 9B
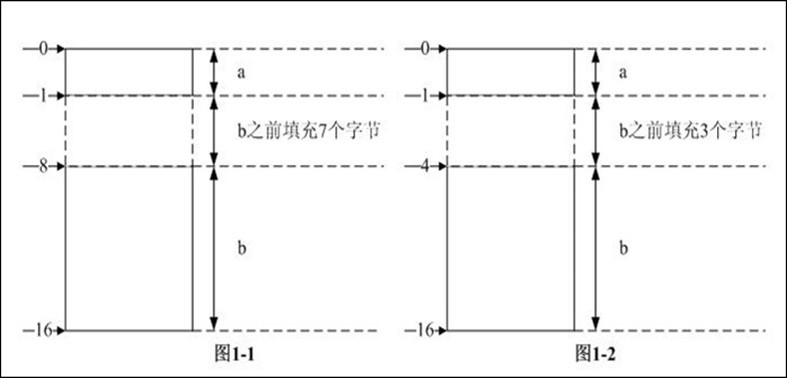
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是8，之前需填充7个字节，sum_a + 7 = 16B --> sum_b = 16 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为4，所以结构体对齐模数是4。sum_b是4的4倍，不需再次对齐。 （这里我觉得有问题，4是怎么来的，我觉得应该是8，下来还是16）
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图1-1所示。

在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 12B = 13B --> sum_a = 13B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是4，之前需填充3个字节，sum_a + 3 = 16B --> sum_b = 16 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为12后者为4，所以结构体对齐模数是4。sum_b是4的4倍，不需再次对齐。
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图1-2所示。



例子2：
#pragma pack(2)
struct my_struct
{
char a;
long double b;
};
#pragma pack()
例子1和例子2不同之处在于例子2中使用了#pragma pack(2)编译参数，它强制指定对齐模数是2。此例子Windows和Linux计算方法有些许不一致。

在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B = 13B --> sum_a = 9B
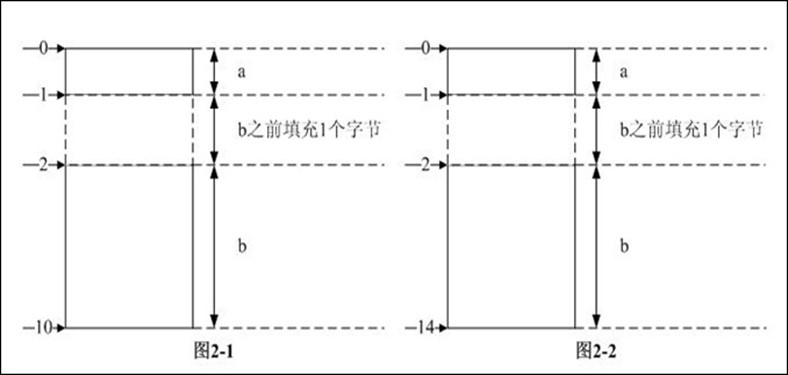
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是2，之前需填充1个字节，sum_a + 1 = 10B --> sum_b = 10 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为2，所以结构体对齐模数是2。sum_b是2的5倍，不需再次对齐。
综上3步，可知结构体的长度是10B，各数据成员在内存中的分布如图2-1所示。

在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 12B = 13B --> sum_a = 13B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是2，之前需填充1个字节，sum_a + 1 = 14B --> sum_b = 14 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为2，所以结构体对齐模数是2。sum_b是2的7倍，不需再次对齐。
综上3步，可知结构体的长度是14B，各数据成员在内存中的分布如图2-2所示。



例子3：
struct my_struct
{
char a;
double b;
char c;
};
前两例中，数据成员在Linux和Windows下都相同，例3中double的对齐模数在Linux中是4，在Windows下是8，针对这种模数不相同的情况加以分析。
在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B + 1B = 10B --> sum_a = 10B
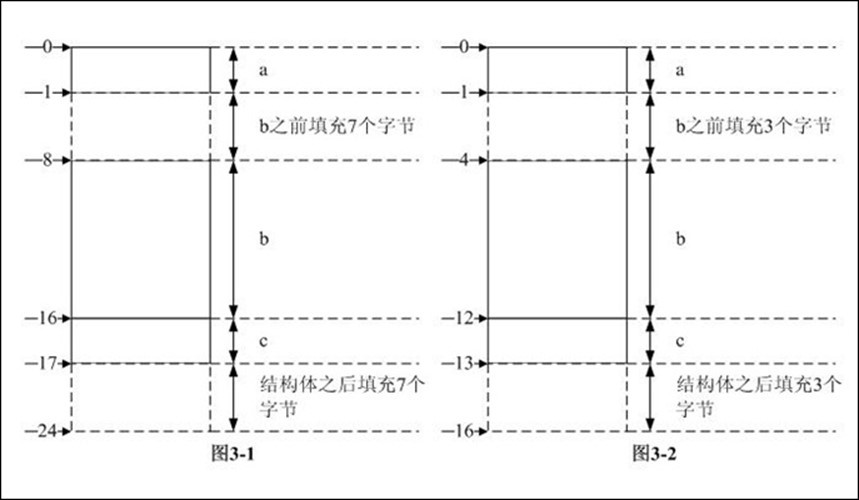
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是8，之前需填充7个字节，sum_a + 7 = 17B --> sum_b = 17B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为8，所以结构体对齐模数是8。sum_b应该是8的整数倍，所以要在结构体后填充8*3 - 17 = 7个字节。
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图3-1所示。

在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B + 1B = 10B，sum_a = 10B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是4，之前需填充3个字节，sum_b = sum_a + 3 = 13B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma
pack中较小者，前者为8后者为4，所以结构体对齐模数是4。sum_b应该是4的整数倍，所以要在结构体后填充4*4 - 13 = 3个字节。
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图3-2所示。



例子4：
struct my_struct
{
char a[11];
int b;
char c;
};
此例子Windows和Linux计算方法一样，如下：
步骤1：所有数据成员自身长度和：11B + 4B + 1B = 16B --> sum_a = 16B
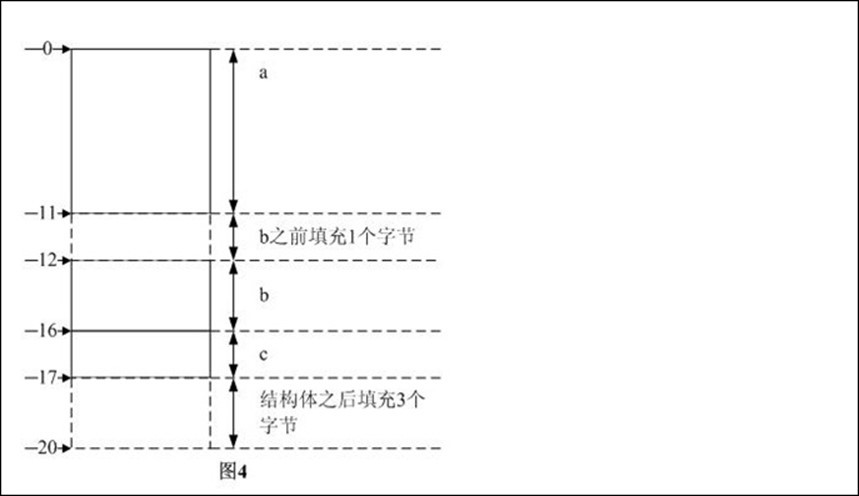
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是4，之前需填充3个字节，sum_a + 1 = 17B --> sum_b = 17B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为4后者为4，所以结构体对齐模数是4。sum_b是4的整数倍，需在结构体后填充4*5 - 17 = 1个字节。
综上3步，可知结构体的长度是20B，各数据成员在内存中的分布如图4所示。



例子5：
struct my_test
{
int my_test_a;
char my_test_b;
};
struct my_struct
{
struct my_test a;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
例子5和前几个例子均不同，在此例子中我们要计算struct my_struct的大小，而my_struct中嵌套了一个my_test结构体。这种结构体应该如何计算呢？原则是将my_test在my_struct中先展开，然后再计算，即是展开成如下结构体：
struct my_struct
{
int my_test_a;
char my_test_b;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
此例子Windows中的计算方法如下：
步骤1：所有数据成员自身长度和：4B + 1B + 8B + 4B + 1B= 18B --> sum_a = 18B
步骤2：数据成员my_struct_a为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是8，之前需填充3个字节：sum_a + 3 = 21B --> sum_b = 21B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为8，所以结构体对齐模数是8。sum_b是8的整数倍，需在结构体后填充3*8 - 21 = 3个字节。
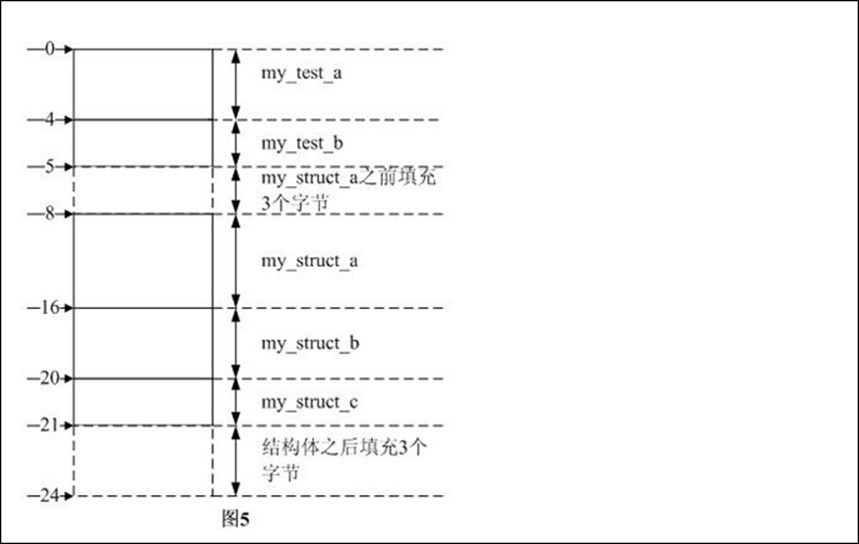
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图5所示。

此例子Linux中的计算方法如下：
步骤1：所有数据成员自身长度和：4B + 1B + 8B + 4B + 1B= 18B，sum_a = 18B
步骤2：数据成员my_struct_a为了内存对齐，根据"结构体大小的计算方法和步骤"中第二条原则，其对齐模数是4，之前需填充3个字节，sum_b = sum_a + 3 = 21B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma
pack中较小者，前者为4后者为4，所以结构体对齐模数是4。sum_b是4的整数倍，需在结构体后填充6*4 - 21 = 3个字节。
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图5所示。


5 -- 源代码附录
上面的例子均在Windows(VC++6.0)和Linux(GCC4.1.0)上测试验证。下面是测试程序。
#include <iostream>

int main()
{
//////////////////////////////////////////////////////////////////////////////////////////
// 例子1
{
struct my_struct
{
char a;
long double b;
};
std::cout << "exapmle-1: sizeof(my_struct) = " << sizeof(my_struct) << std::endl;

struct my_struct data;

printf("my_struct->a: %u\n"
"my_struct->b: %u\n"
"sizeof(long double): %u\n", &data.a, &data.b, sizeof(long double));

}
//////////////////////////////////////////////////////////////////////////////////////////
// 例子2
{
#pragma pack(2)
struct my_struct
{
char a;
long double b;
};
#pragma pack()
struct my_struct data;

std::cout << "exapmle-2: sizeof(my_struct) = " << sizeof(my_struct) << std::endl;

printf("my_struct->a: %u\n"
"my_struct->b: %u\n"
"sizeof(long double): %u\n", &data.a, &data.b, sizeof(long double));
}
//////////////////////////////////////////////////////////////////////////////////////////
// 例子3
{
struct my_struct
{
char a;
double b;
char c;
};

struct my_struct data;

std::cout << "exapmle-3: sizeof(my_struct) = " << sizeof(my_struct) << std::endl;

printf("my_struct->a: %u\n"
"my_struct->b: %u\n"
"my_struct->c: %u\n", &data.a, &data.b, &data.c);
}

//////////////////////////////////////////////////////////////////////////////////////////
// 例子4
{
struct my_struct
{
char a[11];
int b;
char c;
};

std::cout << "example-4: sizeof(my_struct) = " << sizeof(struct my_struct) << std::endl;

struct my_struct data;
printf("my_struct->a: %u\n"
"my_struct->b: %u\n"
"my_struct->c: %u\n", &data, &data.b, &data.c);
}

//////////////////////////////////////////////////////////////////////////////////////////
// 例子5
{
struct my_test
{
int my_test_a;
char my_test_b;
};
struct my_struct
{
struct my_test a;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
std::cout << "example-5: sizeof(my_struct) = " << sizeof(struct my_struct) << std::endl;

struct my_struct data;
printf("my_struct->my_test_a : %u\n"
"my_struct->my_test_b : %u\n"
"my_struct->my_struct_a: %u\n"
"my_struct->my_struct_b: %u\n"
"my_struct->my_struct_c: %u\n", &data.a.my_test_a, &data.a.my_test_b,
&data.my_struct_a, &data.my_struct_b, &data.my_struct_c);

}


return 0;
}